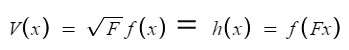Grade 12: Math 30-1, Lessons

Studying a centered parabola for stretches is not as useful as the shifted case.

Let's look at the case where the parabola is asymmetrical to the y-axis and has two roots. Notice: - Horizontal contraction does not preserve the roots, the x of the vertex, and thus does not preserve the axis of symmetry. - Horizontal contraction preserves the y of the vertex, the y-intercept. - Horizontal transformations are not propagating from the parabola's axis of symmetry, they anchor rather on the y-inetrcept (try this on the graph). - Vertical dilation preserves the roots, the x of the vertex and thus the axis of symmetry. - Vertical dilation does not preserve the y-intercept, y of the vertex,

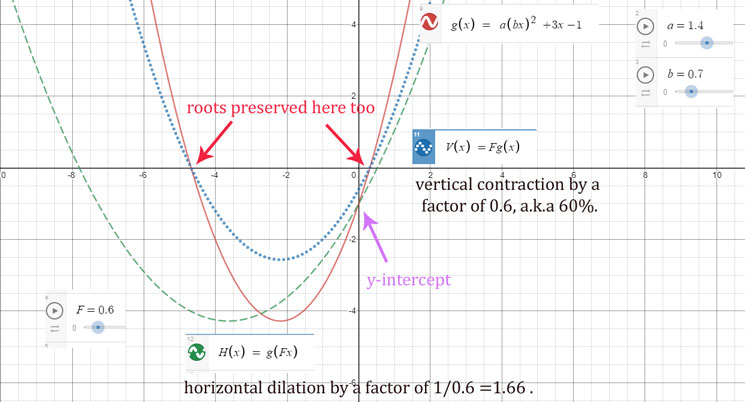
After changing the factor from F = 2 to F = 0.6, what was a contraction earlier becomes a dilation and vice versa. Regardless of the factor, the same elements are preserved as listed above. Play with the factor F in this graph (click on the image to do so) and see what is affected. This will help you develop your intuition. Notice also in contractions/dilations that it is the geometric distances to the axes that are contracted/dilated rather the Cartesian coordinates.

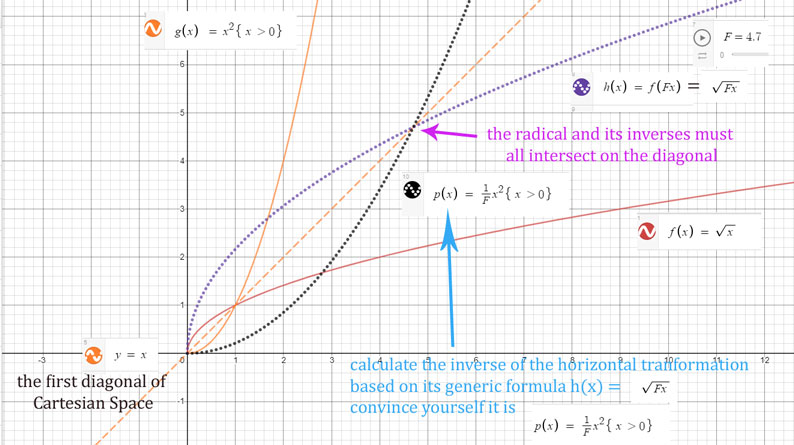
Do Radicals Behave Similarly to Parabolas During Stretches?
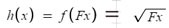
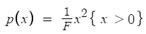
Click on the graph to experiment with the transformation factor F. It is easy to see the parallel between the horizontal stretches of the radical and the same mapping of F in the resultinng inverse Therefore,
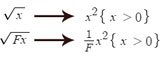
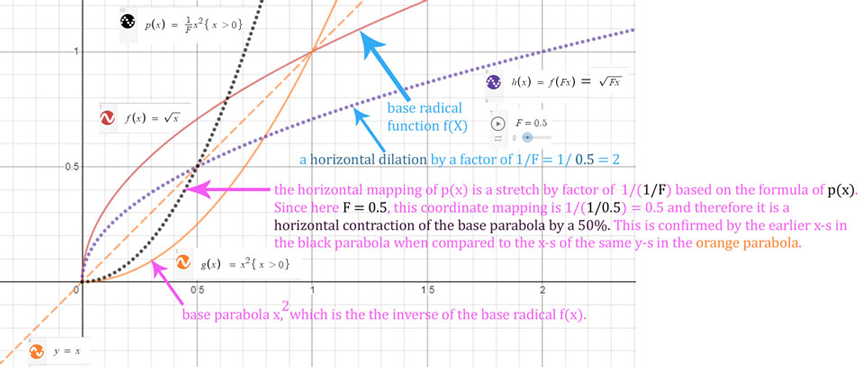
When tracking transformations to the radical function, you can match these changes on the parabolas that are the inverses of these transformations, i.e A horizontal dilation by a factor of 2 in the radical (see comments on the graph) is mirrored by a horizontal contraction by a factor of 0.5 in the matching inverse parabola. To generalize: A horizontal stretch (dilation or contraction) by a factor of 1/F in the radical is mirrored by an horizontal stretch by a factor of F in the matching inverse parabola. Where the radical contracts the parabola dilates and vice versa. This makes sense as it is the only way these parabola - radical pairs maintain the same distance from the mirroring diagonal y = x.

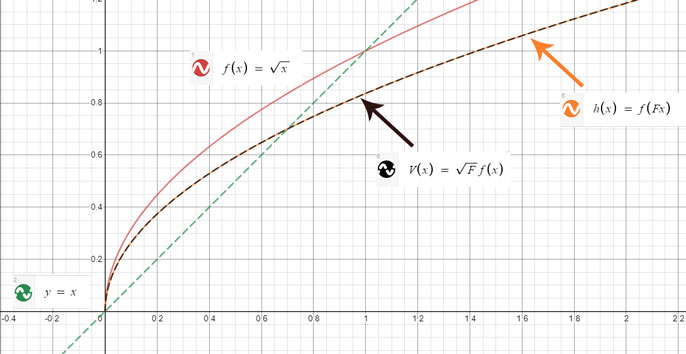
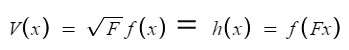
Vertical vs. Horizontal stretches of a radical. In this case the vertical formula and this horizontal formula is identical. Experiment with the graph to see that the dotted black curve is always the same as the orange one.
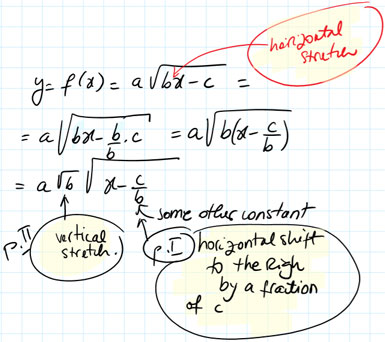
How about more comples formulas under the radical? - any horizontal factor can be converted into a vertical one and vice versa when it comes to radicals. But vertical stretches are easier to deal with because the factor of their mapping (i.e. on the coordinates) is the same as the factor used by the function transformation. In other words (x, y) -> (x, Fy) and v(x) = Ff(x) While in contracts the horizontal mappings are by a factor of 1/F: (x, y) -> (x, 1/F y), when the horizontal transformation function definition is h(x) = Ff(x) In other words, these two factors are reciprocal rather than identical so attention is need to get the correct conclusion in horizontal cases. 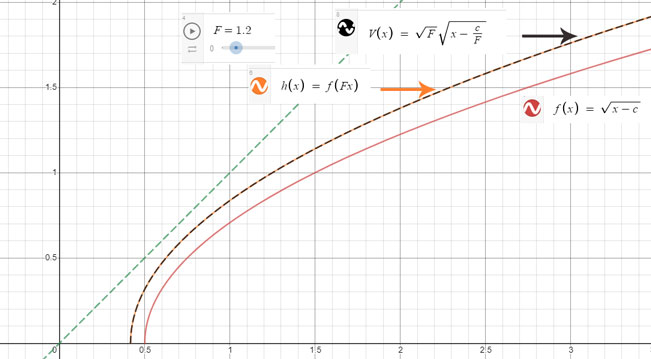Click on the graph to play with the factor F and see that the two - vertical and horizontal - (orange and black respectively) overalp. Therefore instead of dealing w/the horizontal version, just process the vertical one.

Academix: Study, Explore, Engage...

Stretching parabolas

Do Radicals Behave Similarly to Parabolas During Stretches?