Academix
A Non-profit Organization to Help Students Study, Explore, and Engage
Brackets, A Prelude to Factoring Polynomials...
A factor distributes itself as a product to all terms
found inside the brackets. We do this to expand the expression and get
rid of the brackets.
In this example "a" is a variable, the triangle and square represent numbers.
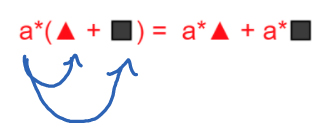
Let's call this the expanded form.
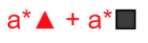
and the left side is the more compact form.
 .
.

“a” is multiplied in both expressions. Whenever that’s the case, you can extract “a” in front of the brackets.
You may need to review the GCF (Greatest Common Factor) and other concepts from earlier grades.
To extract all the factors that are possible in an expression, you can quickly use the GCF (numbers combined with variables too) and position it like the “a” in the example.
But there are other ways, while slower, it is important to illuminate the process:
For example:
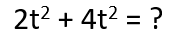
It should be clear that by adding 2 somethings to 4 somethings we get 6 somethings, which in this case are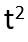 .
.
The answer is thus:
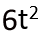
We must get this same answer using a different method: extracting factors in front of brackets, and will allow
us to verify the correctness of the algorithm.
So let's start over, but now using brackets.
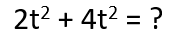
To identify common factors in the constants of this expression, we must first decompose them into primes as follows.
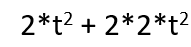
2 is a common factor in both terms, don’t care for now that it is not a GCF. It is marked below for removal, it will be placed outside brackets which we'll add in a moment.
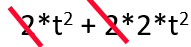
Create brackets for 2 as a factor and place 2 outside the brackets.
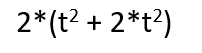
Make sure this 2 does not appear both outside and inside the brackets.
Ask yourself are you finished, or are there still common factors inside the brackets that could be retrieved?
The answer is t is still a factor. If we repeat the process, we'll start by formatting the expression inside the brackets to emphasize the factor .
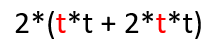
Again we mark t for removal outside the brackets
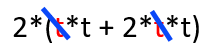
Extract t:
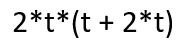
Ask yourself again, are you finished? Are there still some factors inside the brackets that could be retrieved?
There is still another t that is a common factor.
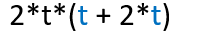
since t can be written as t*1 this formats the first t as a product too:
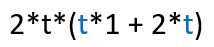
Strike out the t so it can exit the brackets.
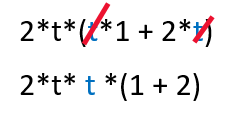
The brackets are (1+2) = 3, and there is such a thing a mathematical etiquette, which dictates that politely all numbers should appear in the from of the term, so then we get:
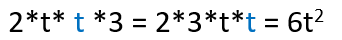
While this was a "funny" example just to show the algorithm of extracting factors on something very simple, try the method on the following examples.
If you can organize the terms in an expanded expression as products with the greatest common factor, the process becomes faster and efficient
In this example "a" is a variable, the triangle and square represent numbers.
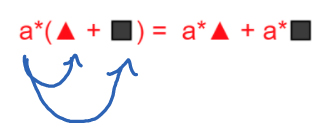
Let's call this the expanded form.
and the left side is the more compact form.
Now learn to recognize this in reverse so you can create brackets instead.

“a” is multiplied in both expressions. Whenever that’s the case, you can extract “a” in front of the brackets.
You may need to review the GCF (Greatest Common Factor) and other concepts from earlier grades.
To extract all the factors that are possible in an expression, you can quickly use the GCF (numbers combined with variables too) and position it like the “a” in the example.
But there are other ways, while slower, it is important to illuminate the process:
For example:
It should be clear that by adding 2 somethings to 4 somethings we get 6 somethings, which in this case are
The answer is thus:
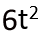
We must get this same answer using a different method: extracting factors in front of brackets, and will allow
us to verify the correctness of the algorithm.
So let's start over, but now using brackets.
To identify common factors in the constants of this expression, we must first decompose them into primes as follows.
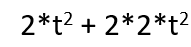
2 is a common factor in both terms, don’t care for now that it is not a GCF. It is marked below for removal, it will be placed outside brackets which we'll add in a moment.
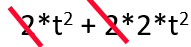
Create brackets for 2 as a factor and place 2 outside the brackets.
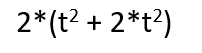
Make sure this 2 does not appear both outside and inside the brackets.
Ask yourself are you finished, or are there still common factors inside the brackets that could be retrieved?
The answer is t is still a factor. If we repeat the process, we'll start by formatting the expression inside the brackets to emphasize the factor .
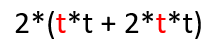
Again we mark t for removal outside the brackets
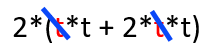
Extract t:
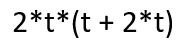
Ask yourself again, are you finished? Are there still some factors inside the brackets that could be retrieved?
There is still another t that is a common factor.
since t can be written as t*1 this formats the first t as a product too:
Strike out the t so it can exit the brackets.
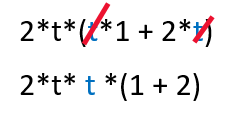
The brackets are (1+2) = 3, and there is such a thing a mathematical etiquette, which dictates that politely all numbers should appear in the from of the term, so then we get:
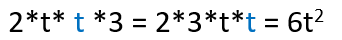
While this was a "funny" example just to show the algorithm of extracting factors on something very simple, try the method on the following examples.
If you can organize the terms in an expanded expression as products with the greatest common factor, the process becomes faster and efficient
Factor the expression 6mn + 3m to get a more compacted bracketed expression.
| The slow way, | The solution using the GCF |
6mn + 3m = extract 3: 3*2mn + 3*m = 3*(2mn + m) = extract m: 3*(m*2n + m) = second m needs a product too: 3*(m*2n + m*1) = 3m*(2n + 1) The two terms in the brackets have no other common factors, so we are finished. |
all the prime (and variable factors) of the first term: 2*3*m*n all the prime (and variable factors) of the second term: 3*m The common factors in 2*3*m*n and 3*m are: 3*m, thus the GCF gets passed in the front of the brackets 6mn + 3m = 2*3*m*n + 3*m = rearrange a bit 3m*2n + 3m= but then the second term has no product so we give it one: 3m*2n + 3m*1= 3m(2n + 1) The two terms in the brackets have no other common factors, so we are finished. |
Factor the expression 18w - 12 to get a more compacted bracketed expression.
| The solution using the GCF |
| all the prime (and variable factors) of the first term: 2*3*3*w all the prime (and variable factors) of the second term: 2*2*3 The common factors in 2*3*3*w and 2*2*3 are: 2*3, thus the GCF gets passed in the front of the brackets 18w - 12 = 2*3*3*w + 2*2*3 = 2*3*3w + 2*3*2 = 2*3*(3w+2) = 6(3w + 2) The two terms in the brackets have no other common factors, so we are finished. |
MORE PRACTICE
| Practice the GCF of polynomials: | https://ca.ixl.com/math/grade-10/gcf-of-monomials |
| Extract a monomial (i.e. one term) as a factor: | https://ca.ixl.com/math/grade-10/factor-out-a-monomial |
| Polynomials - Greatest Common Factor | https://www.analyzemath.com/high_school_math/grade_11/common_factor_sol.html |
Academix: Study, Explore, Engage...
Copyright © 2025 Academix. All Rights Reserved.