Radicals and Square Roots

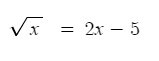it represents the intersection of a radical function on the left side of the equation (blue below) with the line (green below) on the right side of the equation.

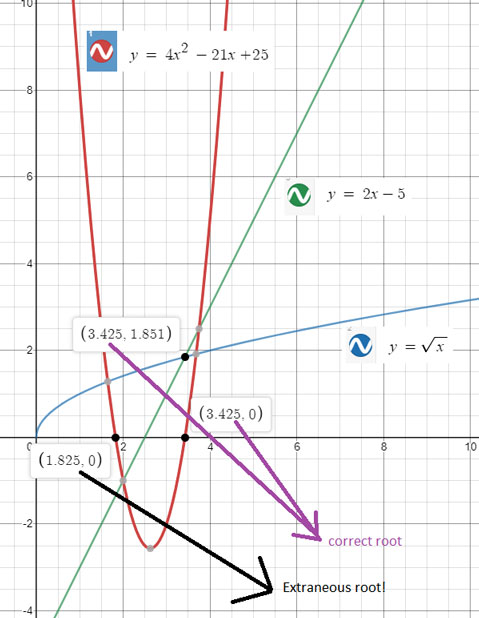
The graph shows clearly the two intersect in only one point: x=3.425.

To solve this we typically square both sides to get:

and as a result consolidate a quadratic equation as shown below.

But then we are no longer working with the described intersection but rather with a parabola and its roots, a.k.a. x-intercepts (red below).

Notice with the parabola only one of its roots solves the original radical equation. The second root (x = 1.825) is introduced during the finding the parabola's roots. We call this non-solving root Extraneous to the original equation.

In another example, can you predict that the next equation has no solution?

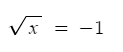
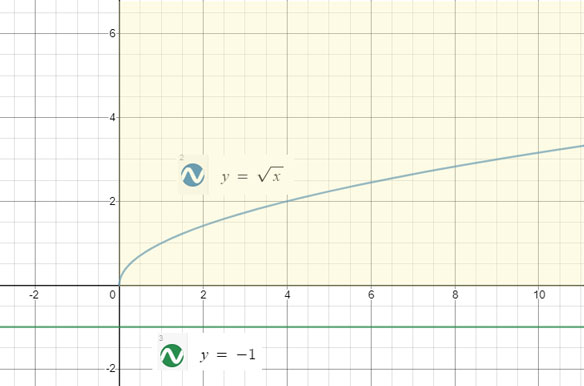
By graphing the left and right sides of the equation separately and seeing the solution as the intersection of the two sides of the equation, we can observe below that the two sides have no commonalities, and thus will never intersect. The radical (left side of the equation) exists only in the first quadrant (highlighted area), while the right side of the equation, the line y = -1, passes below the graph without ever touching the first quadrant. Therefore there are no solutions to this equation, as shown below.

The traditional way to attempt to solve this equation is to square both its sides, like so:

from here we derive that

x = 1

However, this is only an extraneous solution that solves the equivalent step after squaring but not the original equation.

In conclusion, whenever using the squaring method to get rid of a radical/square root in an equation, we must always verify al the solutions to make sure they are not extraneous.

Introduction to Radicals, Lesson Math 20-1

(direct PDF download: https://www.sachs.gsacrd.ab.ca/eteacher_download/992/24978)

Exponents and Radicals on shelovesmath.com

Radical Equations and Inequalities

Evaluating Statements about Radicals, Lesson plan (this link downloads the PDF directly: from https://www.map.mathshell.org/download.php?fileid=1714)

Radicals on lamar.edu: http://tutorial.math.lamar.edu/Classes/Alg/Radicals.aspx

Academix: Study, Explore, Engage...