Polynomials and Factoring


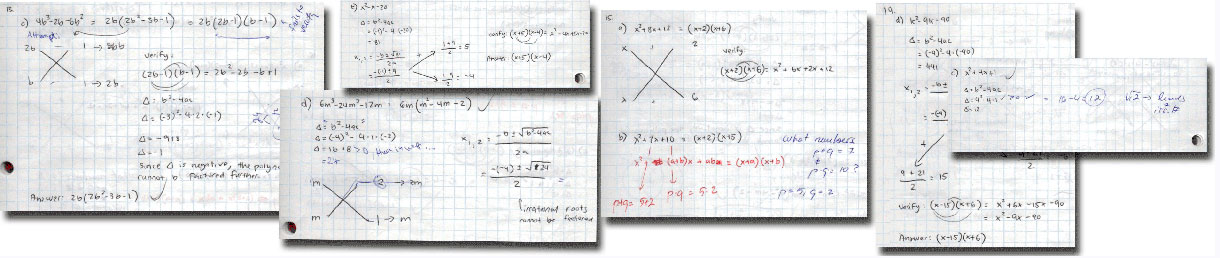
Polynomials
Lessons	http://tutorial.math.lamar.edu/Classes/Alg/Polynomials.aspx

Polynomial Functions	http://carlisleschools.ss13.sharpschool.com/cms/One.aspx?portalId=95563&pageId=768777

What is the difference between algebraic and arithmetic fractions?	https://www.math-only-math.com/arithmetic-fraction-and-algebraic-fraction.html


Polynomials, Factoring
Before you begin working on this concept: Part I	How do brackets work? Brackets are an important concept to factorization. Practice extracting simple factors out in front of brackets. Example First, a factor distributes to all elements in the brackets when expanding the expression. 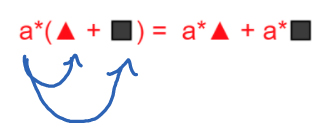Learn to recognize this in reverse: “a” is multiplied in both expressions. Recognize it as a factor that can play its role in front of brackets. Practice creating brackets from simple expressions. Click here if you have difficulty with this part...

Before you begin working on this concept: Part II	Recognizing the major algebraic formulas in reverse is very useful in factorizing polynomials as it gives immediate results. For example: a² - b² should be immediately recognized in its factorized form simply based on the formula (a+b)(a-b) Or for example should always be recognized as
	Example: The Factoring Lemma is useful when we want to simplify a rational polynomial quickly. For the following fraction to simplify we would need (x-2) to divide the denominator. No other than (x-2) would be interesting here since this is the only thing in the numerator. A quick check of p(2) shows = 0 and it thus becomes clear the denominator is divisible by (x-2). This knowledge helps factorize the denominator faster.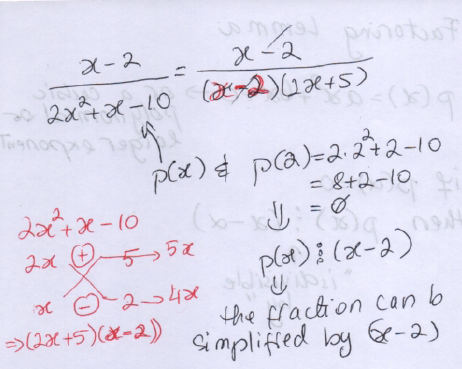
Polynomials, Factoring slide show
Factoring Methods	http://www.shelovesmath.com/algebra/intermediate-algebra/factoring-quadratics-and-completing-the-square/#FactoringMethods
Factoring Methods, Advanced	http://www.shelovesmath.com/algebra/advanced-algebra/advanced-factoring/

What is Factorizing Polynomials?	More on Factorizing Polynomials here.
Divisibility of numbers is a useful concept for factoring polynomials:	Quick ways to determine divisibility: A number is divisible by 2 if it terminates with 2, 4, 6, 8, or 0. A number is divisible by 3 if the sum of its digits is divisible by 3. A number is divisible by 4 if the last two digits are divisible by 4. A number is divisible by 5 if it terminates with 5 or 0. A number is divisible by 6 if it is divisible by both 2 and 3. A number is divisible by 8 if the last three digits are divisible by 8. A number is divisible by 9 if the sum of digits is divisible by 9. A number is divisible by 10 if it terminates with 0.
Worksheet 2.6 Factorizing Algebraic Expressions (PDF Download)
Lectures and Practice	https://www.khanacademy.org/math/algebra/polynomial-factorization

Factoring Trinomials Tips and Tricks
Practice and solutions	http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx

Art of Problem Solving: Simon's Favorite Factoring Trick
Criss Cross Method (why does it work?)
Factoring Trinomials
Dividing Polynomials
Polynomials, Synthetic Division
Various Calculators on Wolfram	https://www.wolframalpha.com/examples/mathematics/algebra/
Factoring Calculator on Wolfram https://www.wolframalpha.com/input/?i=6x%5E2+-+x+-+2

This page is sponsored by Sharp Book Series

Academix: Study, Explore, Engage...

Polynomials

Polynomials, Factoring

How do brackets work?